Using the Jump Diffusion Model to Describe Rotation

In last two lectures we learned the basics of diffusion and how to describe the diffusion flux using Ficks first J -D and second law D where D is defined as the diffusion coefficient D see Lecture 3 which hasRT an SI unit of m²s length²time. Table 1 summarizes the different values obtained for the orientational relaxation times either from experiments if available from our MD simulations from the diffusive model with the OH rotational diffusion constant calculated from our MD simulations independently of any consideration of the jumps from jump model calculations using the.

Method To Extract Multiple States In F1 Atpase Rotation Experiments From Jump Distributions Pnas

Function gduupt du1 u1 end prob SDEProblemfg0200100 and couple it to the jumps.

. The steps are the same as before except we now start with a SDEProblem instead of an ODEProblem. T the jump times and then simulating geometric Brownian motion on intervals between jump times. U t is the value of the jump.

However the BNS jump test technique shows that the jump definitely happen for every day which is contrary to the conclusion from Merton jump diffusion model based on intraday data of SPY. Jump-diffusion models have been introduced by Robert C. Tic processes can be generated using simulation methods and examplify the fact that Jump-Diffusion models are improvements from classical Black-Scholes-Merton model to incorporate the fat tail effects usually exhibited in empricial financial data.

In a Merton jump diffusion model the prices evolve between the jumps like a geometric Brownian motion and after each jump the value of St is multiplied by eYi St S0 exp µ s2 2t sBt Nt å i1 Yi. 2 The Normal Jump-Diffusion Model. Jump-diffusion process but with respect to application of the broader model to pricing bonds the Gaussian and jump parameters seem sensitive to estimation technique as well as the proxy used for the short rate where applicable.

The resulting model can be used to derive other series of interest such as the default probability and the credit spread. Where Nt t 0 is a Poisson process with intensity l and the jump sizes Yt t 0 a sequence of iid normally distributed rv. The SDE 1 has the exact solution.

This equation corresponds to 28 with the addition of a jump term and is a particular case of the general jump-diffusion model 14 15 when γ t y y. A GBM model has two parameters. Both the double expo-nential and normal jump-diffusion models can lead to the leptokurtic feature although the kurtosis from the double exponential jump-diffusion model.

The revised jump-diffusion and rotation-diffusion model rJRM is an improved model to fit QENS spectra collected on four cement pastes at temperatures 210 - 280 K within E between -120 and 120 μeV and Q from 03 to 19 Å-1. ε is the diffusion. The proposed technique is simulated using a 2D electromagnetic forward modeler which is described in Section 2.

In Section 3 we describe the application of jump-diffusion algorithm for building estimation. It is calculated by σNORMSINV RAND where sigma is the standard deviation of the jumps. Jump-diffusions as a valuable tool in their day-to-day modeling.

In option pricing a jump-diffusion model is a form of mixture model mixing a jump process and a diffusion process. In Mertons paper Ys are normally distributed. I am trying to understand the difference between using Jump diffusion model and Neural Networks or more precisely LSTM to predict time series data regardless what that data contains for example a stock price or withdrawals from ATMs.

Merton as an extension of jump models. Creating a Jump-Diffusion Model. The misspecified jump-diffusion model badly overestimates the jump probability and.

A jump in the structural jump-diffusion model corresponds to a sudden change in the asset value that may or may not cause the firm to default whereas a jump in the reduced-form model represents the default event itself. I is equal to 0 for no jump or 1 for a jump. Although both the structural jump-diffusion model and the reduced-form model contain jumps these jumps have different meanings.

Exponential jump-diffusion model fits stock data bet-ter than the normal jump-diffusion model. This increasing interest to jump models in finance is mainly due to the following reasons. Now we will finally solve the jump diffusion problem.

DS α µ - Φ K m - ln S S dt σ S dz K S dq. E x e r T S T K I max 0 t T S. Due to their computational tractability the special case of a basic affine jump diffusion is popular for some credit risk and short.

75 The jump diffusion model proposed by Chudley and Elliott CE 76 is commonly used to describe the scattering from interstitial H atoms diffusing through a. Clewlow et al 2001b. The value is determined by the jump probability.

First in a model with continuous paths like a diffusion model the price process behaves locally like a Brownian motion and the probability that the. But the Monte Carlo evidence also shows that a sample size of 2000daily observations for a decadeis not large enough to pin down the parameters of the jump distribution accurately. On the other hand in order to identify jumps the jumps based on intraday prices I introduce BCH method.

Consider an up-and-in call option and assume that the price of the underlying asset follows a jump-diffusion model then under certain conditions the price of an up-and-in call with barrier H S 0 x strike K and maturity T is given by the following expectation. The diffusion process is supposed to account for small day-to-day asset returns due to the arrival at an efficient market of information that has only a minor impact on the assets equilibrium. In what follows we shall thus consider the more general version of 31 given by 32 d S t S t μ t d t σ t d w t γ t Y t d N t.

With mean m and standard deviation s. The simplest mean-reversion jump-diffusion model for spot prices is described by the following equation Clewlow and Strickland 2000. Section 2 reviews the derivation of the PDDE implied by ATSMs that include a jump-diffusion process for the short.

Risk-neutral drift If the above model is used as a pricing model the. S t S 0 exp t Z t 2 t2 J t 2 Merton 6 considers the case where the jump sizes Y iare normally distributed. Merton 1976 was the first to consider a jump-diffusion model similar to 1 and 3.

In Section 4 we develop the scalable approach were low resolution estimates are used to initiate more refined estimation. The drift average trend and the diffusion volatility of. 1999 demonstrate empirically that for the SP 500 data from 1980-1996 the normal jump-diffusion model has a much higher p-value 00152 than those of the stochastic volatility model 00008 and the Black-Scholes model.

If I look at research papers I will find examples of Jump Diffusion model and LSTM to predict stock prices. Jump-diffusion models are based on the standard geometric Brownian motion GBM diffusion model. This follows a normal distribution.

Tions more closely Press 9 proposed a model that is a combination of a Gauss-Wiener diffusion process and an independent Poisson-driven jump process. Model looks pretty good for the stochastic volatility equation. Using the same drift function f as before we add multiplicative noise via.

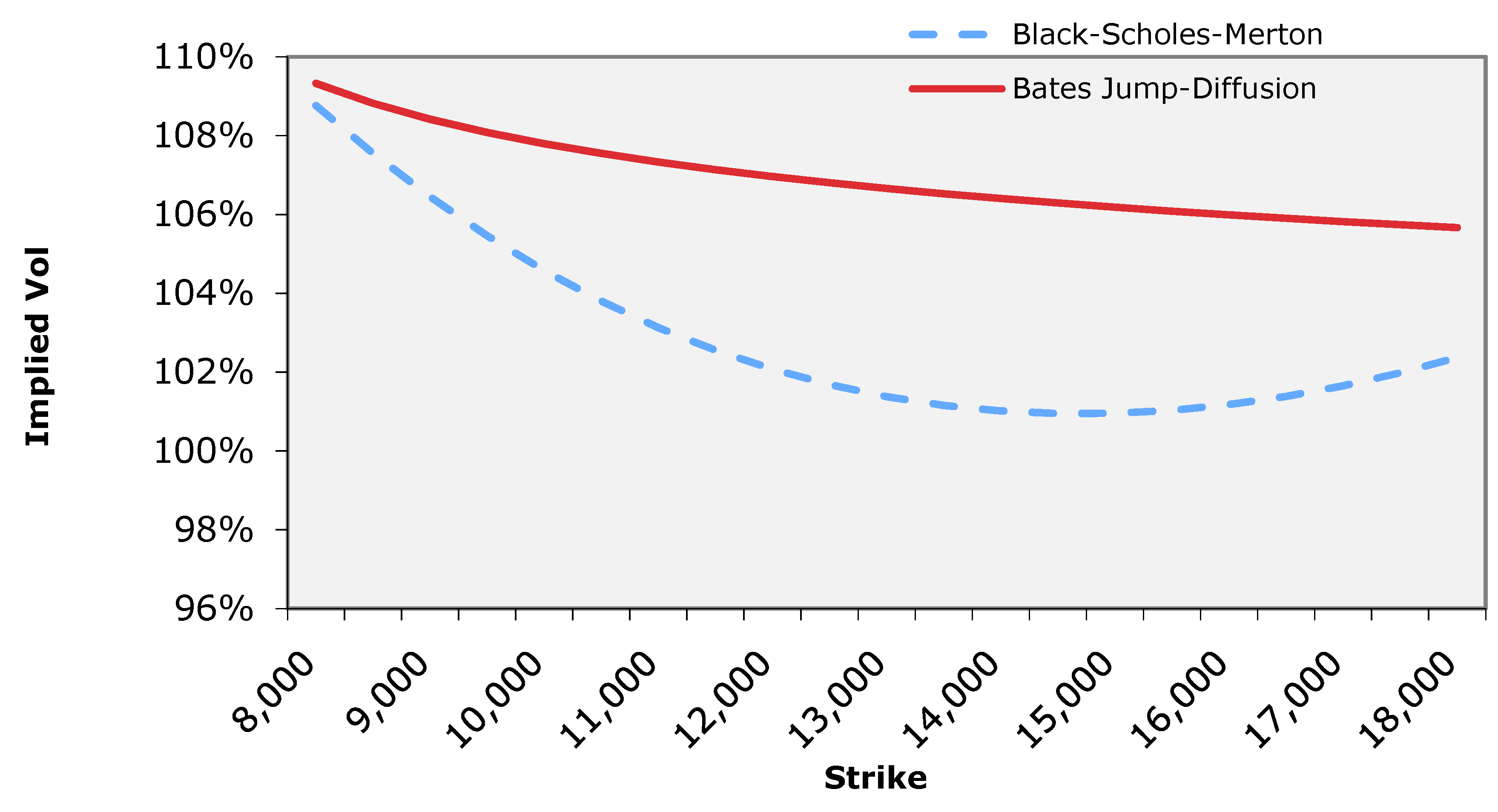
Mathematics Free Full Text Detecting Jump Risk And Jump Diffusion Model For Bitcoin Options Pricing And Hedging Html

Diffusion Model An Overview Sciencedirect Topics

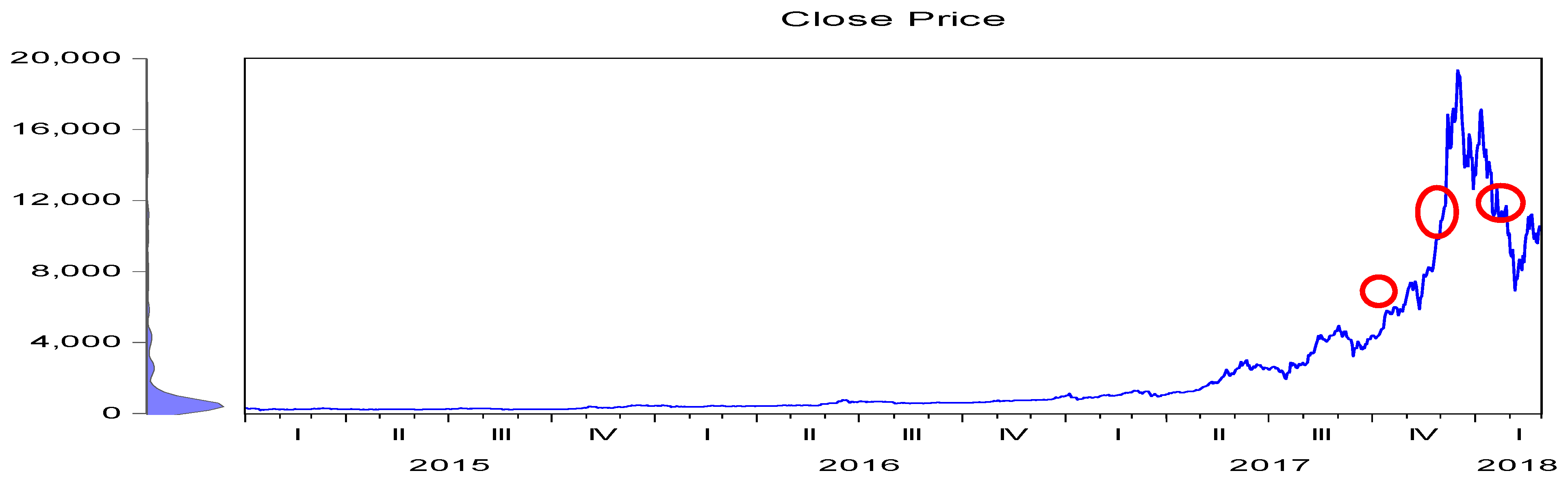
Mathematics Free Full Text Detecting Jump Risk And Jump Diffusion Model For Bitcoin Options Pricing And Hedging Html